Để học tốt Toán 8, phần này giúp bạn giải các bài tập trong sách giáo khoa Toán 8 được biên soạn bám sát theo nội dung sách Toán 8.
Trả lời câu hỏi Toán 8 Tập 1 Bài 10 trang 26: Làm tính chia
a) x3 : x2;
b) 15x7 : 3x2;
c) 20x5 : 12x.
Lời giải
a) x3 : x2 = x(3 – 2) = x1 = x
b) 15x7 : 3x2 = (15 : 3).(x7 : x2 )= 5.x(7-2) = 5x5

Lời giải
a) 15x2y2 : 5xy2 = (15:5).(x2 : x).(y2 : y2 ) = 3.x(2-1).1 = 3x

Bài 59 (trang 26 SGK Toán 8 Tập 1): Làm tính chia trong các bài 59, 60, 61:

Lời giải:

Kiến thức áp dụng
Với hai số tự nhiên m, n và m > n ta có: am : an = am – n
Với b ≠ 0 ta có: am : bm = (a : b)m
Bài 60 (trang 27 SGK Toán 8 Tập 1): Làm tính chia trong các bài 59, 60, 61:
a) x10 : (-x)8
b) (-x)5 : (-x)3
c) (-y)5 : (-y)4
Lời giải:
a) x10 : (-x)8 = x10 : x8 = x10 – 8 = x2
Vì (-x)8 = (-1.x)8 = (-1)8.x8 = x8
b) (-x)5 : (-x)3 = (-x)5 – 3 = (-x)2 = x2
Vì (-x)2 = (-1.x)2 = (-1)2.x2 = x2
c) (-y)5 : (-y)4 = (-y)5 – 4 = (–y)1 = – y
Kiến thức áp dụng
+ Với hai số tự nhiên m, n và m > n ta có: am : an = am – n
+ Với n là số chẵn ta luôn có (–a)n = an
Bài 61 (trang 27 SGK Toán 8 Tập 1): Làm tính chia trong các bài 59, 60, 61:

Lời giải:
a) 5x2y4 : 10x2y
= (5 : 10).(x2 : x2).(y4 : y)
(Chia hệ số cho hệ số, chia lũy thừa của từng biến)

Kiến thức áp dụng
Muốn chia đơn thức A cho đơn thức B ta làm như sau :
+ Chia hệ số của đơn thức A cho hệ số của đơn thức B
+ Chia lũy thừa của từng biến trong A cho lũy thừa của cùng biến đó trong B.
+ Nhân các kết quả vừa tìm được với nhau.
Với mọi số a và các số tự nhiên m, n mà m > n ta có: am : an = am – n.
Bài 62 (trang 37 SGK Toán 8 Tập 1): Tính giá trị của biểu thức 15x4y3z2 : 5xy2z2 tại x = 2, y = – 10 và z = 2004.
Lời giải:
Ta có : 15x4y3z2 : 5xy2z2
= (15 : 5).(x4 : x).(y3 : y2).(z2 : z2)
= 3.x4 – 1.y3 – 2 . 1
= 3x3y
Tại x = 2 ; y = –10 và z = 2004, giá trị biểu thức bằng : 3.23.(–10) = –240.
Kiến thức áp dụng
Muốn chia đơn thức A cho đơn thức B ta làm như sau :
+ Chia hệ số của đơn thức A cho hệ số của đơn thức B
+ Chia lũy thừa của từng biến trong A cho lũy thừa của cùng biến đó trong B.
+ Nhân các kết quả vừa tìm được với nhau.
Với mọi số a và các số tự nhiên m, n mà m > n ta có: am : an = am – n.
Lý thuyết & Bài tập Bài 10 có đáp án: Chia đơn thức cho đơn thức
A. Lý thuyết
1. Đơn thức chia cho đơn thức
Với A và B là hai đơn thức, B≠0. Ta nói A chia hết cho B nếu tìm được một đơn thức Q sao cho A = B.Q.
Trong đó:
A là đơn thức bị chia.
B là đơn thức chia.
Q là đơn thức thương (hay gọi là thương)

2. Quy tắc
Nhớ lại kiến thức cũ: Ở lớp 7 ta biết: Với x≠0; m, n ∈ N; m ≥ n thì:
xm : xn = xm – n nếu m>n
xm : xn = 1 nếu m=n
(xn)m = xn.m
Quy tắc:
Muốn chia đơn thức A cho đơn thức B (trường hợp A chia hết cho B) ta làm như sau:
+ Chia hệ số của đơn thức A cho hệ số của đơn thức B.
+ Chia lũy thừa của từng biến trong A cho lũy thừa của cùng biến đó trong B.
+ Nhân các kết quả vừa tìm được với nhau.
Ví dụ: Thực hiện phép tính
a, ( – 2 )5 : ( – 2 )3.
b, ( xy2 )4 : ( xy2 )2
Hướng dẫn:
a) Ta có: ( – 2 )5 : ( – 2 )3 = ( – 2 )5 – 3 = ( – 2 )2 = 4.
b) Ta có: ( xy2 )4 : ( xy2 )2 = x4y8 : x2y4 = x4 – 2.y8 – 4 = x2y4.
B. Bài tập tự luyện
Bài 1: Tính giá trị của các biểu thức sau
a) P = 12x4y2 : (- 9xy2 ) tại x= -3, y= 1,005.
b) Q = 3x4y3:2xy2 tại x= 2, y= 1.
Hướng dẫn:
a) Ta có P = 12x4y2 : ( – 9xy2 ) = 1/2 – 9x4 – 1y2 – 2 = – 4/3x3
Với x= -3, y= 1,005 ta có P = – 4/3( – 3 )3 = 36.
Vậy P = 36
b) Ta có Q = 3x4y3:2xy2 = 3/2x4 – 1y3 – 2 = 3/2x3y.
Với x= 2, y= 1 ta có Q = 3/2( 2 )3.1 = 12.
Vậy Q = 12
Bài 2: Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến y (x≠0; y≠0) với biểu thức đó là A = 2/3x2y3🙁 – 1/3xy ) + 2x( y – 1 )( y + 1 )
Hướng dẫn:
Ta có A = 2/3x2y3🙁 – 1/3xy ) + 2x( y – 1 )( y + 1 ) = – 2x2 – 1y3 – 1 + 2x( y – 1 )( y + 1 )
= – 2xy2 + 2x( y2 – 1 ) = – 2xy2 + 2xy2 – 2x = – 2x
⇒ Giá trị của biểu thức A không phụ thuộc vào biến y
Trắc nghiệm Chia đơn thức cho đơn thức (có đáp án)
Bài 1: Kết quả của phép chia 15x3y4 : 5x2y2 là
A. 3xy2
B. -3x2y
C. 5xy
D. 15xy2
Lời giải
Ta có 15x3y4 : 5x2y2 = (15 : 5).(x3 : x2).(y4 : y2) = 3xy2.
Đáp án cần chọn là: A
Bài 2: Thương của phép chia (-xy)6 : (2xy)4 bằng:
A. (-xy)2
B. (xy)2
C. (2xy)2
D.
Lời giải

Đáp án cần chọn là: D
Bài 3: Chia đơn thức (-3x)5 cho đơn thức (-3x)2 ta được kết quả là
A. -9x3
B. 9x3
C. 27x3
D. -27x3
Lời giải
Ta có (-3x)5 : (-3x)2 = (-3x)3 = (-3)3.x3 = -27x3
Đáp án cần chọn là: D
Bài 4: Thương của phép chia (-12x4y + 4x3 – 8x2y2) : (-4x)2 bằng
A. -3x2y + x – 2y2
B. 3x4y + x3 – 2x2y2
C. -12x2y + 4x – 2y2
D. 3x2y – x + 2y2
Lời giải
(-12x4y + 4x3 – 8x2y2) : (-4x)2
= (-12x4y) : (-4x2) + (4x3) : (-4x2) – (8x2y2) : (-4x2)
= 3x2yy – x + 2y2
Bài 5: Kết quả của phép chia (2x3 – x2 +10x) : x là
A. x2 – x + 10
B. 2x2 – x + 10
C. 2x2 – x – 10
D. 2x2 + x + 10
Lời giải
Ta có (2x3 – x2 +10x) : x
= (2x3 : x) – (x2 : x) + (10x : x) = 2x2 – x + 10
Đáp án cần chọn là: B
Bài 6: Kết quả của phép chia (6xy2 + 4x2y – 2x3) : 2x là
A. 3y2 + 2xy – x2
B. 3y2 + 2xy + x2
C. 3y2 – 2xy – x2
D. 3y2 + 2xy
Lời giải
(6xy2 + 4x2y – 2x3) : 2x
= 6xy2 : 2x + 4x2y : 2x – 2x3 : 2x
= 3y2 + 2x – x2
Đáp án cần chọn là: A
Bài 7: Chia đa thức (3x5y2 + 4x3y2 – 8x2y2) cho đơn thức 2x2y2 ta được kết quả là

Lời giải
Ta có (3x5y2 + 4x3y2 – 8x2y2) : 2x2y2
= (3x5y2 : 2x2y2) + (4x3y2 : 2x2y2) – (8x2y2 : 2x2y2)
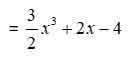
Đáp án cần chọn là: B
Bài 8: Chia đa thức (4x2yz4 + 2x2y2z2 – 3xyz) cho đơn thức xy ta được kết quả là
A. 4xz4 + 2xyz2 – 3z
B. 4xz4 + 2xyz2 + 3z
C. 4xz4 – 2xyz2 + 3z
D. 4xz4 + 4xyz2 + 3z
Lời giải
Ta có (4x2yz4 + 2x2y2z2 – 3xyz) : xy
= (4x2yz4 : xy) + (2x2y2z2 : xy) – (3xyz : xy)
= 4xz4 + 2xyz2 – 3z
Đáp án cần chọn là: A
Bài 9: Chọn câu đúng
A. 24x4y3 : 12x3y3 = 2xy
B. 18x6y5 : (-9x3y3) = 2x3y2
C. 40x5y2 : (-2x4y2) = -20x
D. 9a3b4x4 : 3a2b2x2 = 3ab3x2
Lời giải
Ta có
+) 24x4y3 : 12x3y3 = (24 : 12).(x4 : x3).(y3 : y3) = 2x nen A sai
+) 18x6y5 : (-9x3y3) = (18 : (-9)).(x6 : x3).(y5 : y3 = -2x3y2 nên B sai
+) 40x5y2 : (-2x4y2) = (40 : (-2)).(x5 : x4).(y2 : y2) = -20x nên C đúng
+) 9a3b4x4 : 3a2b2x2 = (9 : 3).(a3 : a2).(b4 : b2).(x4 : x2) = 3ab2x2 nên D sai
Đáp án cần chọn là: C
Bài 10: Chọn câu đúng
A. 20x5y3 : 4x2y2 = 5x3y2

Bài 11: Chọn câu sai
A. (3x – y)7 : (y – 3x)2 = -(3x – y)5
B. (x – y)5 : (x – y)2 = (x – y)3
C. (2x – 3y)9 : (2x – 3y)6 = (2x – 3y)3
D. (x – 2y)50 : (x – 2y)21 = (x – 2y)29
Lời giải
Ta có
+) (3x – y)7 : (y – 3x)2 = (3x – y)7 : (3x – y)2 = (3x – y)5 nên A sai
+) (x – y)5 : (x – y)2 = (x – y)5-2 = (x – y)3 nên B đúng
+) (2x – 3y)9 : (2x – 3y)6 = (2x – 3y)9-6 = (2x – 3y)3 nên C đúng
+) (x – 2y)50 : (x – 2y)21 = (x – 2y)50-21 = (x – 2y)29 nên D đúng
Đáp án cần chọn là: A
Bài 12: Chọn câu sai
A. (-15x2y6) : (-5xy2) = 3xy4
B. (8x5 – 4x3) : (-2x)3 = -4x2 + 2

Bài 13: Chọn câu đúng
A. Thương của phép chia đa thức (a6x3 + 2a3x4 – 9ax5) cho đơn thức ax3 là a5 + 2a2x – 9x2
B. Thương của phép chia đa thức (a6x3 + 2a3x4 – 9ax5) cho đơn thức ax3y phép chia hết
C. Thương của phép chia đa thức (a6x3 + 2a3x4 – 9ax5) cho đơn thức ax3 là a5 + 2a2x + 9x2
D. Thương của phép chia đa thức (a6x3 + 2a3x4 – 9ax5) cho đơn thức ax3 là a5x + 2a2x – 9x2Hiển thị đáp án
Lời giải
Ta có
+) (a6x3 + 2a3x4 – 9ax5) : ax3
= (a6x3 : ax3) + (2a3x4 : ax3) – (9ax5 : ax3)
= a5 + 2a2x – 9x2
Nên A đúng, C, D sai
+) Phép chia đa thức (a6x3 + 2a3x4 – 9ax5) cho đơn thức ax3y không là phép chia hết vì đa thức (a6x3 + 2a3x4 – 9ax5) không có biến y nên B sai
Đáp án cần chọn là: A
Bài 14: Chọn câu đúng nhất

C. Cả A, B đều đúng
D. Cả A, B đều sai
Lời giải
Ta có

Bài 15: Cho A = (3a2b)3(ab3)2; B = (a2b)4. Khi đó A : B bằng
A. 27ab5
B. -27b5
C. 27b5
D. 9b5
Lời giải
Ta có A = (3a2b)3(ab3)2 = 33.(a2)3.b3.a2(b3)2
= 27a6.b3.a2.b6 = 27a8b9
B = (a2b)4 = (a2)4.b4 = a8b4
Khi đó A : B = 27a8b9 : a8b4 = 27b5
Đáp án cần chọn là: C
Bài 16: Cho A = (4x2y2)2(xy3)3; B = (x2y3)2. Khi đó A : B bằng
A. 16x4y6
B. 8x3y8
C. 4x3y7
D. 16x3y7
Lời giải
Ta có A = (4x2y2)2(xy3)3 = 42(x2)2(y2)2x3(y3)3 = 16x4y4x3y9 = 16x7y13
B = (x2y3)2 = (x2)2(y3)2 = x4y6
Khi đó A : B = 16x7y13 : x4y6 = 16x3y7
Đáp án cần chọn là: D
Bài 17: Cho (2x+ y2).(…) = 8x3 + y6. Điền vào chỗ trống (…) đa thức thích hợp
A. 2x2 – 2xy + y4
B. 2x2 – 2xy + y2
C. 4x2 – 2xy2 + y4
D. 4x2 + 2xy + y4
Lời giải
Ta có 8x3 + y6 = (2x)3 + (y2)3
= (2x + y2)((2x)2 – 2x.y2 + (y2)2)
= (2x + y2)(4x2 – 2xy2 + y4)
Vậy đa thức cần điền là 4x2 – 2xy2 + y4
Đáp án cần chọn là: C
Bài 18: Cho (3x – 4y).(…) = 27x3 – 64y3. Điền vào chỗ trống (…) đa thức thích hợp
A. 6x2 + 12xy + 8y2
B. 9x2 + 12xy + 16y2
C. 9x2 – 12xy + 16y2
D. 3x2 + 12xy + 4y2
Lời giải
Ta có
27x3 – 64y3 = (3x)3 – (4y)3 = (3x – 4y)((3x)2 + 3x.4y + (4y)2)
= (3x – 4y)(9x2 + 12xy + 16)
Vậy đa thức cần điền là 9x2 + 12xy + 16
Đáp án cần chọn là: B
Bài 19: Cho (27x3 + 27x2 + 9x + 1) : (3x + 1)2 = (…) Điền vào chỗ trống đa thức thích hợp
A. (3x + 1)5
B. 3x + 1
C. 3x – 1
D. (3x + 1)3
Lời giải
Ta có
(27x3 + 27x2 + 9x + 1) : (3x + 1)2 = (3x + 1)3 : (3x + 1)2 = 3x + 1
Đáp án cần chọn là: B
Bài 20: Cho (7x4 – 21x3) : 7x2 + (10x + 5x2) : 5x = (…). Điền vào chỗ trống đa thức thích hợp
A. x2 – 2x + 2
B. x2 – 4x + 2
C. x2 – x + 5
D. x2 – 2x + 5
Lời giải
Ta có
(7x4 – 21x3) : 7x2 + (10x + 5x2) : 5x =
= 7x4 : (7x2) – 21x3 : (7x2) + 10x : (5x) + 5x2 : (5x)
= x2 – 3x + 2 + x
= x2 – 2x + 2
Đáp án cần chọn là: A
Bài 21: Giá trị số tự nhiên n để phép chia xn : x6 thực hiện được là:
A. n Є N, n < 6
B. n Є N, n ≥ 6
C. n Є N, n > 6
D. n Є N, n ≤ 6
Lời giải
Để phép chia xn : x6 thực hiện được thì n Є N, n – 6 ≥ 0 ⇔ n ≥ 6, n Є N
Đáp án cần chọn là: B
Bài 22: Giá trị số tự nhiên n để phép chia x2n : x4 thực hiện được là:
A. n Є N, n > 2
B. n Є N, n ≥ 4
C. n Є N, n ≥ 2
D. n Є N, n ≤ 2Hiển thị đáp án
Lời giải
Để phép chia x2n : x4 thực hiện được thì n Є N, 2n – 4 ≥ 0 ⇔ n ≥ 2, n Є N
Đáp án cần chọn là: C
Bài 23: Giá trị số tự nhiên n thỏa mãn điều kiện gì để phép chia xn+3y6 : x9yn là phép chia hết?
A. n < 6
B. n = 5
C. n > 6
D. n = 6Hiển thị đáp án
Lời giải
Để phép chia xn+3y6 : x9yn là phép chia hết thì

Đáp án cần chọn là: D
Bài 24: Tìm điều kiện của số tự nhiên n (n > 0) để đơn thức B = 4x4y4 chia hết đơn thức C = xn-1y4 là
A. n = 5
B. 0 < n ≤ 5
C. n ≥ 5
D. n = 0
Lời giải
Ta có B : C = (4x4y4) : (xn-1y4)
Đơn thức B chia hết cho đơn thức C khi 4 ≥ n – 1 ⇒ n ≤ 5
Hay 0 < n ≤ 5
Đáp án cần chọn là: B
Bài 25: Giá trị biểu thức A = 15x5y4z3 : (-3x4y4z2) với x = -2; y = 2004; z = 10 là
A. -100
B. 100
C. -200
D. 120Hiển thị đáp án
Lời giải
Ta có A = 15x5y4z3 : (-3x4y4z2) = (15 : (-3)).(x5 : x4).(y4 : y4).(z3 : z2) = -5xz
Thay x = -2; y = 2004; z = 10 vào A = -5xz ta có
A = -5.(-2).10 = 100
Đáp án cần chọn là: B
Bài 26: Tính giá trị của biểu thức D = (15xy2 + 18xy3 + 16y2) : 6y2 – 7x4y3 : x4y tại x=2/3 và y = 1

Lời giải
D = (15xy2 + 18xy3 + 16y2) : 6y2 – 7x4y3 : x4y
⇔ D = 15xy2 : (6y2) + 18xy3 : (6y2) + 16y2 : (6y2) – 7x4y3 : x4y

Bài 27: Thương của phép chia (9x4y3 – 18x5y4 – 81x6y5) : (-9x3y3) là đa thức có bậc là:
A. 5
B. 9
C. 3
D. 1Hiển thị đáp án
Lời giải
Ta có (9x4y3 – 18x5y4 – 81x6y5) : (-9x3y3)
= [(9x4y3) : (-9x3y3)] – [18x5y4 : (-9x3y3)] – [81x6y5 : (-9x3y3)]
= -x + 2x2y + 9x3y2
Đa thức -x + 2x2y + 9x3y2 có bậc 3 + 2 = 5
Đáp án cần chọn là: A
Bài 28: Biểu thức D = (9x2y2 – 6x2y3) : (-3xy)2 + (6x2y + 2x4) : (2x2) sau khi rút gọn là đa thức có bậc là
A. 1
B. 3
C. 4
D. 2Hiển thị đáp án
Lời giải
D = (9x2y2 – 6x2y3) : (-3xy)2 + (6x2y + 2x4) : (2x2)
⇔ D = 9x2y2 : (-3xy)2 – 6x2y3 : (-3xy)2 + 6x2y : (2x2) + 2x4 : : (2x2)

Bài 29: Chọn kết luận đúng về giá trị của biểu thức

A. Giá trị của biểu thức không phụ thuộc biến x
B. Giá trị của biểu thức không phụ thuộc biến y
C. Giá trị của biểu thức không phụ thuộc biến
D. Giá trị của biểu thức không phụ thuộc vào cả hai biến x, y
Lời giải


Bài 31: Cho A = x5yn – 12xn+1y4; B = 24xn-1y3. Tìm số tự nhiên n > 0 để A ⁝ B
A. n Є {3;4;5;6}
B. n Є {4;5;6}
C. n Є {1;2;3;4;5;6}
D. n Є {4;5}
Lời giải
Ta có A : B = (x5yn – 12xn+1y4) : (24xn-1y3)
= (x5yn) : (24xn-1y3) – (12xn+1y4) : (24xn-1y3)


✅ Giải bài tập sách giáo khoa toán 8 ⭐️⭐️⭐️⭐️⭐️
Mọi chi tiết liên hệ với chúng tôi :
TRUNG TÂM GIA SƯ TÂM TÀI ĐỨC
Các số điện thoại tư vấn cho Phụ Huynh :
Điện Thoại : 091 62 65 673 hoặc 01634 136 810
Các số điện thoại tư vấn cho Gia sư :
Điện thoại : 0902 968 024 hoặc 0908 290 601

Leave a Reply