Mục lục bài viết
Để học tốt Toán 8, phần này giúp bạn giải các bài tập trong sách giáo khoa Toán 8 được biên soạn bám sát theo nội dung sách Toán 8.
Trả lời câu hỏi Toán 8 Tập 1 Bài 3 trang 72: Hình thang ABCD (AB // CD) trên hình 23 có gì đặc biệt ?
Lời giải
Hình thang ABCD trên hình 23 có hai góc kề cạnh đáy lớn bằng nhau
Trả lời câu hỏi Toán 8 Tập 1 Bài 3 trang 72: Cho hình 24.
a) Tìm các hình thang cân.
b) Tính các góc còn lại của mỗi hình thang cân đó.
c) Có nhận xét gì về hai góc đối của hình thang cân ?

Lời giải
a)
+) Hình 24a) có: ˆA+ˆC=80°+100°=180°
Mà hai góc ở vị trí trong cùng phía nên AB//DC
Suy ra ABDC là hình thang.
Hình thang ABDC có ˆA=ˆB=80°
Suy ra ABDC là hình thang cân.
+) Hình 24b) tứ giác EFGH không là hình thang nên cũng không là hình thang cân.


Trả lời câu hỏi Toán 8 Tập 1 Bài 3 trang 74: Cho đoạn thẳng CD và đường thẳng m song song với CD (h.29). Hãy vẽ các điểm A, B thuộc m sao cho ABCD là hình thang có hai đường chéo CA, DB bằng nhau. Sau đó hãy đo các góc ˆC và ˆD của hình thang ABCD đó để dự đoán về dạng của các hình thang có đường chéo bằng nhau.

Lời giải
Muốn xác định hai điểm A, B trên m ta lần lượt quay cung tròn tâm C bán kính R cắt đường thẳng m tại A và cung tròn tâm D bán kính R cắt đường thẳng m tại B.
Ta được hình thang ABCD.

Sau khi tiến hàng đo, ta thấy hai góc C và D bằng nhau
Từ đó ta có dự đoán sau: Hình thang có hai đường chéo bằng nhau là hình thang cân.
Bài 11 (trang 74 SGK Toán 8 Tập 1): Tính độ dài các cạnh của hình thang cân ABCD trên giấy kẻ ô vuông (h.30, độ dài của cạnh ô vuông là 1cm).

Lời giải:

(Mỗi ô vuông là 1cm).
Ta lấy điểm E như trên hình vẽ.
Quan sát vào hình vẽ ta thấy :
+ AB = 2cm
+ CD = 4cm.
+ Tính AD :
Xét tam giác vuông ADE có AE = 1cm, DE = 3cm:
AD2 = AE2 + DE2 (Định lý Pytago)
AD2 = 12 + 32 = 10
⇒AD=√10cm.
+ Tính BC:
ABCD là hình thang cân nên AD=BC=√10cm
Vậy các cạnh của hình thang lần lượt là: AB = 2cm, CD = 4cm, AD=BC=√10cm
.Kiến thức áp dụng
+ Định lý Pytago: Tam giác ABC vuông tại A ⇔ AB2 + AC2 = BC2.
+ Trong hình thang cân, hai cạnh bên bằng nhau.
Bài 12 (trang 74 SGK Toán 8 Tập 1): Cho hình thang cân ABCD (AB // CD, AB < CD). Kẻ các đường cao AE, BF của hình thang. Chứng minh rằng DE = CF.
Lời giải:


Vì hình thang ABCD cân
AD = BC;
Ĉ = D̂
Xét hai tam giác vuông AED và BFC có:
AD = BC
Ĉ = D̂
⇒ ΔAED = ΔBFC (cạnh huyền – góc nhọn)
⇒ DE = CF.
Kiến thức áp dụng
Trong hình thang cân:
+ Hai góc ở đáy bằng nhau
+ Hai cạnh bên bằng nhau.
Bài 13 (trang 74 SGK Toán 8 Tập 1): Cho hình thang cân ABCD (AB//CD), E là giao điểm của hai đường chéo. Chứng minh rằng EA = EB, EC = ED.
Lời giải:

Do ABCD là hình thang cân nên:
AD = BC;
AC = BD;
Xét hai tam giác ADC và BCD, ta có:
AD = BC (gt)
AC = BD (gt)
DC cạnh chung
⇒ ΔADC = ΔBCD (c.c.c)

⇒ ΔECD cân tại E
⇒ EC = ED.
Mà AC = BD
⇒ AC – EC = BD – ED
hay EA = EB.
Vậy EA = EB, EC = ED.
Kiến thức áp dụng
Trong một hình thang cân:
+ Hai đường chéo bằng nhau
+ Hai cạnh bên bằng nhau.
Bài 14 (trang 75 SGK Toán 8 Tập 1): Đố. Trong các tứ giác ABCD, EFGH trên giấy kẻ ô vuông (h.31), tứ giác nào là hình thang cân? Vì sao?

Lời giải:
Ta quy ước mỗi ô vuông có cạnh 1cm.

+ Xét tứ giác ABCD
Nhận thấy AB // CD ⇒ Tứ giác ABCD là hình thang.
Xét ΔACK vuông tại K, có AK = 4 cm, CK = 1cm:
AC2 = AK2 + KC2 (định lý Py – ta – go)
AC2 = 42 + 12 = 17
Xét ΔBHD vuông tại H, có BH = 4 cm, HD = 1cm:
BD2 = BH2 + HD2 (định lý Py – ta – go)
BD2 = 42 + 12 = 17
⇒ AC2 = BD2
⇒ AC = BD
Vậy hình thang ABCD có hai đường chéo AC = BD nên là hình thang cân.
+ Xét tứ giác EFGH
FG // EH ⇒ Tứ giác EFGH là hình thang.
Lại có : EG = 4cm
Xét ΔFIH vuông tại I, có HI = 3 cm, IF = 2cm:
FH2 = IH2 + IF2 (định lý Py – ta – go)
FH2 = 32 + 22 = 13
⇒FH=√13cm.
⇒FH≠EG
Vậy hình thang EFGH có hai đường chéo không bằng nhau nên không phải hình thang cân.
Kiến thức áp dụng
+ Để chứng minh một hình thang là hình thang cân, ta sử dụng một trong các cách sau:
– Chứng minh hai góc kề một đáy bằng nhau
– Chứng minh hai đường chéo bằng nhau
+ Định lý Pytago: ΔABC vuông tại A ta luôn có: AB2 + AC2 = BC2.
Bài 15 (trang 75 SGK Toán 8 Tập 1): Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy theo thứ tự các điểm D, E sao cho AD = AE
a) Chứng minh rằng BDEC là hình thang cân.
b) Tính các góc của hình thang cân đó, biết rằng góc A = 50o.
Lời giải:


Mà hai góc ở vị trí đồng vị ⇒ DE // BC
⇒ Tứ giác DECB là hình thang.
Mà hai góc ở đáy B và C bằng nhau nên hình thang DECB là hình thang cân.
b)

Kiến thức áp dụng
+ Tính chất: Trong một hình thang cân, hai góc kề một đáy bằng nhau.
+ Để chứng minh một hình thang là hình thang cân, ta sử dụng một trong các cách sau:
– Chứng minh hai góc kề một đáy bằng nhau.
– Chứng minh hai đường chéo bằng nhau.
Bài 16 (trang 75 SGK Toán 8 Tập 1): Cho tam giác ABC cân tại A, các đường phân giác BD, CE (D ∈ AC, E ∈ AB). Chứng minh rằng BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.
Lời giải:

Chứng minh tứ giác BCDE là hình thang cân:

Kiến thức áp dụng
+ Tính chất: Trong một hình thang cân, hai góc kề một đáy bằng nhau.
+ Để chứng minh một hình thang là hình thang cân, ta sử dụng một trong các cách sau:
– Chứng minh hai góc kề một đáy bằng nhau.
– Chứng minh hai đường chéo bằng nhau.
Bài 17 (trang 75 SGK Toán 8 Tập 1): Hình thang ABCD (AB // CD) có
Chứng minh rằng ABCD là hình thang cân.
Lời giải:


Vậy hình thang ABCD có hai đường chéo AC = BD nên là hình thang cân.
Kiến thức áp dụng
Để chứng minh một hình thang là hình thang cân, ta sử dụng một trong các cách sau:
– Chứng minh hai góc kề một đáy bằng nhau.
– Chứng minh hai đường chéo bằng nhau.
Bài 18 (trang 75 SGK Toán 8 Tập 1): Chứng minh định lý: “Hình thang có hai đường chéo bằng nhau là hình thang cân” qua bài toán sau: Cho hình thang ABCD (AB // CD) có AC = BD. Qua B kẻ đường thẳng song song với AC, cắt đường thẳng DC tại tại E. Chứng minh rằng:
a) ΔBDE là tam giác cân.
b) ΔACD = ΔBDC
c) Hình thang ABCD là hình thang cân.
Lời giải:



Kiến thức áp dụng
+ Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau, hai cạnh đáy bằng nhau.
+ Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
Bài 19 (trang 75 SGK Toán 8 Tập 1): Đố. Cho ba điểm A, D, K trên giấy kẻ ô vuông (h.32) Hãy tìm điểm thứ tư M giao điểm của các dòng kẻ sao cho nó cùng với ba điểm đã cho là bốn đỉnh của một hình thang cân.

Lời giải:
Ta có thể xác định hai điểm M thỏa mãn như dưới hình.

Lý thuyết & Bài tập Bài 3 có đáp án: Hình thang cân
A. Lý thuyết
1. Định nghĩa
Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.

2. Tính chất
Định lí 1: Trong một hình thang cân, hai cạnh bên bằng nhau, ABCD là hình thang cân (đáy AB, CD) ⇒ AD = BC
Định lí 2: Trong một hình thang cân, hai đường chéo bằng nhau, ABCD là hình thang cân (đáy AB, CD) ⇒ AC = BD
Định lí 3: Hình thang có hai đường chéo bằng nhau là hình thang cân. Hình thang ABCD (đáy AB, CD) có AC = BD ⇒ ABCD là hình thang cân.
3. Dấu hiệu nhận biết
Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.
Hình thang có hai đường chéo bằng nhau là hình thang cân.
B. Ví dụ minh họa
Ví dụ : Cho hình thang cân ABCD (AB // CD, AB < CD ). Kẻ các đường cao AE, BF của hình thang. Chứng minh rằng DE = CF.
Hướng dẫn:

Ta có ABCD là hình thang cân nên AD = BC
+ Xét tam giác vuông ADE có
AD2 = AE2 + DE2 ⇒ DE2 = AD2 – AE2 ⇔ DE = √( AD2 – AE2 ) ( 1 )
+ Xét tam giác vuông BCF có:
BC2 = BF2 + CF2 ⇒ CF2 = BC2 – BF2 ⇔ CF = √( BC2 – BF2 ) ( 2 )
Xét tứ giác ABFE có AB// EF nên là hình thang. Lại có hai cạnh bên AE// BF (cùng vuông góc CD ) nên AE = BF (3)
Từ ( 1 ), ( 2 ) và ( 3 ) ⇒ DE = CF (do AD = BC và AE = BF )
B. Bài tập tự luyện
Bài 1: Cho hình thang cân ABCD( AB//CD,AB < CD ). Kẻ đường cao AH,BK của hình thang. Chứng minh rằng DH = CK.
Hướng dẫn:

Áp dụng định nghĩa, tính chất và giả thiết của hình thang cân ta có:

⇒ Δ ADH = Δ BCK
(trường hợp cạnh huyền – góc nhọn)
⇒ DH = CK (cặp cạnh tương ứng bằng nhau)
Vậy DH = CK. (đpcm)
Bài 2: Tính các góc của hình thang cân, biết có một góc bằng 600
Hướng dẫn:

Do góc A và góc D là hai góc cùng nằm một phía của
AB//CD nên chúng bù nhau hay Aˆ + Dˆ = 1800.
⇒ Aˆ = 1800 – Dˆ = 1800 – 600 = 1200.
Do đó Aˆ = Bˆ = 1200.
Vậy Cˆ = Dˆ = 600 và Aˆ = Bˆ = 1200.
✅ Giải bài tập sách giáo khoa toán 8 ⭐️⭐️⭐️⭐️⭐️
Mọi chi tiết liên hệ với chúng tôi :
TRUNG TÂM GIA SƯ TÂM TÀI ĐỨC
Các số điện thoại tư vấn cho Phụ Huynh :
Điện Thoại : 091 62 65 673 hoặc 01634 136 810
Các số điện thoại tư vấn cho Gia sư :
Điện thoại : 0902 968 024 hoặc 0908 290 601

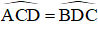
Leave a Reply