Công thức tính thể tích hình nón cụt

Công thức tính thể tích, diện tích xung quanh, diện tích toàn phần của khối nón cụt

Công thức xác định thể tích, diện tích xung quanh và diện tích toàn phần của khối nón cụt.

Nhằm giúp các em có công thức xác định nhanh các yêu cầu tính thể tích hay diện tích xung quanh của khối nón cụt, bài viết này hệ thống hoá công thức tính để các em tham khảo. 

Xét khối nón cụt có R,r,h lần lượt là bán kính đáy lớn, bán kính đáy nhỏ và chiều cao ta có

1. Tính diện tích hình nón cụt

Diện tích hình nón cụt thường được nhắc đến với 2 khái niệm: diện tích xung quanh và diện tích toàn phần.

1.1. Tính diện tích xung quanh hình nón cụt

Diện tích xung quanh hình nón cụt chỉ bao gồm diện tích mặt xung quanh, bao quanh hình nón cụt, không gồm diện tích hai đáy. Công thức tính diện tích xung quanh: bằng hiệu diện tích xung quanh của hình nón lớn và hình nón nhỏ.

1.2. Tính diện tích toàn phần hình nón cụt

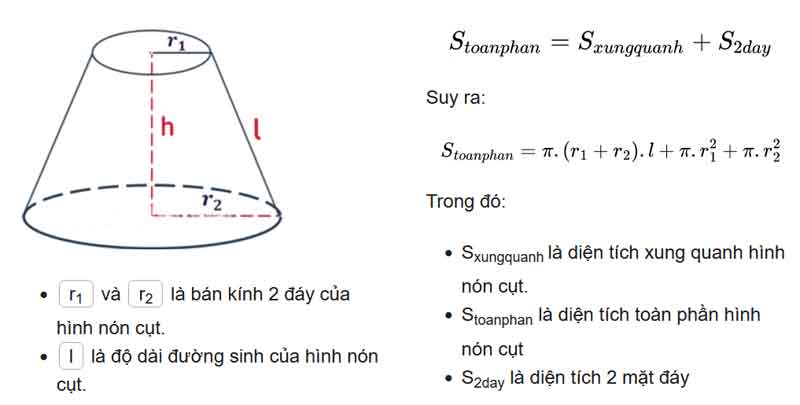
Diện tích toàn phần được tính là độ lớn của toàn bộ không gian hình chiếm giữ, bao gồm cả diện tích xung quanh và diện tích hai đáy tròn.

Công thức tính diện tích toàn phần: bằng diện tích xung quanh cộng với diện tích của 2 đáy.

Tính thể tích hình nón cụt

Thể tích hình nón cụt là lượng không gian mà hình nón cụt chiếm.

Công thức tính thể tích hình nón cụt: bằng hiệu thể tích của hình nón lớn và hình nón nhỏ.

Hình nón cụt là gì?

Khi cắt hình nón bởi một mặt phẳng song song với đáy thì phần mặt phẳng nằm trong hình nón là một hình tròn. Phần hình nằm giữa mặt phẳng nói trên và mặt đáy được gọi là một hình nón cụt.

Có thể hiểu, hình nón cụt là hình có 2 đáy là hai hình tròn có bán kính to nhỏ khác nhau nằm trên hai mặt phẳng song song có đường nối tâm là trục đối xứng.

Khái niệm hình nón cụt

Hình nón cụt được tạo ra từ hình nón như sau: cho tam giác AOC vuông ở O. Khi quay tam giác vuông này một vòng quanh cạnh OA ta sẽ được một hình nón. Cạnh OC quét đáy tạo thành một hình tròn tâm O bán kính OC. Trong khi đó, cạnh AC quét tạo thành mặt xung quanh của hình nón và cạnh AC được gọi là đường sinh của hình nón.

Từ hình nón đã được tạo thành, ta dùng một mặt phẳng song song đáy cắt qua hình nón, ta được một hình nón cụt.

Như vậy, hình nón cụt là hình có 2 đáy là hai hình tròn có bán kính to nhỏ khác nhau nằm trên hai mặt phẳng song song có đường nối tâm là trục đối xứng.

Bài tập

Bài tập 1. Một hình chóp cụt có các thông số như hình vẽ. Hãy tìm thể tích; diện tích xung quanh và diện tích toàn phần của hình chóp cụt này

Lời giải

Từ hình vẽ, ta thấy

Bài tập 2. Một nút chai thủy tinh là một khối tròn xoay (H), một mặt phẳng chứa trục của (H) cắt (H) theo một thiết diện như trong hình vẽ bên. Tính thể tích của (H) (đơn vị cm³).

Hướng dẫn giải

Chọn đáp án C.

Bài tập 3. Cho hai hình vuông có cùng cạnh bằng 5 được xếp chồng lên nhau sao cho đỉnh X của một hình vuông là tâm của hình vuông còn lại (như hình vẽ). Tính thể tích V của vật thể tròn xoay khi quay mô hình trên xung quanh trục XY.

Hướng dẫn giải

Chọn C.

Cách 1 

Bài tập 4. Một cái phễu có dạng hình nón. Người ta đổ một lượng nước vào phễu sao cho chiều cao của lượng nước trong phễu bằng 13 chiều cao của phễu. Hỏi nếu bịt kín miệng phễu rồi lộn ngược phễu lên thì chiều cao của nước bằng bao nhiêu ? Biết rằng chiều cao của phễu là 15cm

Hướng dẫn giải

– Phương pháp: Tính thể tích của phần hình nón không chứa nước, từ đó suy ra chiều cao h′, chiều cao của nước bằng chiều cao phễu trừ đi h′.

GIA SƯ TOÁN