Binomial Theorem

Binomial theorem primarily helps to find the expanded value of the algebraic expression of the form (x + y)ⁿ. Finding the value of (x + y)², (x + y)³, (a + b + c)² is easy and can be obtained by algebraically multiplying the number of times based on the exponent value. But finding the expanded form of (x + y)¹⁷ or other such expressions with higher exponential values involves too much calculation. It can be made easier with the help of the binomial theorem.

The exponent value of this binomial theorem expansion can be a negative number or a fraction. Here we limit our explanations to only non-negative values. Let us learn more about the terms, formula and the properties of coefficients in this binomial expansion article.

What is Binomial Theorem?

The first mention of the binomial theorem was in the 4th century BC by a famous Greek mathematician by name of Euclids. The binomial theorem states the principle for expanding the algebraic expression (x + y)ⁿ and expresses it as a sum of the terms involving individual exponents of variables x and y. Each term in a binomial expansion is associated with a numeric value which is called coefficient.

Statement: According to the binomial theorem, it is possible to expand any non-negative power of binomial (x + y) into a sum of the form,

(x+y)ⁿ = ⁿC₀ xⁿy⁰ + ⁿC₁ x^n-1y¹ + ⁿC₂ x^n-2 y² + … + ⁿC_n-1 x¹y^n-1 + ⁿC_n x⁰yⁿ

where, n ≥ 0 is an integer and each ⁿC_k is a positive integer known as a binomial coefficient.

Note: When an exponent is zero, the corresponding power expression is 1. This multiplicative factor is often omitted from the term, therefore often the right hand side is directly written as ⁿC₀ xⁿ + …. This formula is also referred to as the binomial formula or the binomial identity. Using summation notation, the binomial theorem can be given as,

(x+y)ⁿ = ∑ⁿ_k=0ⁿC_k x^n-ky^k = ∑ⁿ_k=0ⁿC_k x^ky^n-k

Example: Let us expand (x+3)⁵ using the binomial theorem. Here y = 3 and n = 5. Substituting and expanding, we get:

(x+3)⁵ = ⁵C₀ x⁵3⁰ + ⁵C₁ x^5-13¹ + ⁵C₂ x^5-2 3² + ⁵C₃ x^5-3 3³ + ⁵C₄ x^5-4 3⁴ + ⁵C₅ x^5-5 3⁵

= x⁵ + 5 x⁴. 3 + 10 x³ . 9 + 10 x² . 27 + 5x .81 + 3⁵

= x⁵ + 15 x⁴ + 90x³ + 270 x² + 405 x + 243

Binomial Expansion

The binomial theorem is also known as the binomial expansion which gives the formula for the expansion of the exponential power of a binomial expression. Binomial expansion of (x + y)ⁿ by using the binomial theorem is as follows,

(x+y)ⁿ = ⁿC₀ xⁿy⁰ + ⁿC₁ x^n-1y¹ + ⁿC₂ x^n-2 y² + … + ⁿC_n-1 x¹y^n-1 + ⁿC_n x⁰yⁿ

Binomial Theorem Formula

The binomial theorem formula is used in the expansion of any power of a binomial in the form of a series. The binomial theorem formula is (a+b)ⁿ= ∑ⁿ_r=0ⁿC_r a^n-rb^r, where n is a positive integer and a, b are real numbers, and 0 < r ≤ n. This formula helps to expand the binomial expressions such as (x + a)¹⁰, (2x + 5)³, (x – (1/x))⁴, and so on. The binomial theorem formula helps in the expansion of a binomial raised to a certain power. Let us understand the binomial theorem formula and its application in the following sections.

The binomial theorem states: If x and y are real numbers, then for all n ∈ N,

(x+y)ⁿ = ⁿC₀ xⁿy⁰ + ⁿC₁ x^n-1y¹ + ⁿC₂ x^n-2 y² + … + ⁿC_k x^n-ky^k +….+ ⁿC_n x⁰yⁿ

⇒ (x + y)ⁿ = ∑ⁿ_k=0ⁿC_k x^n-ky^k

where, ⁿC_r = n! / [r! (n – r)!]

Binomial Theorem Expansion Proof

Let x, a, n ∈ N. Let us prove the binomial theorem formula through the principle of mathematical induction. It is enough to prove for n = 1, n = 2, for n = k ≥ 2, and for n = k+ 1.

It is obvious that (x +y)¹ = x +y and

(x +y)² = (x + y) (x +y)

= x² + xy + xy + y² (using distributive property)

= x² + 2xy + y²

Thus the result is true for n = 1 and n = 2. Let k be a positive integer. Let us prove the result is true for k ≥ 2.

Assuming (x + y)ⁿ = ∑ⁿ_r=0ⁿC_r x^n-ry^r,

(x + y)^k = ∑^k_r=0^kC_r x^k-ry^r

⇒ (x+y)^k = ^kC₀ x^ky⁰ + ^kC₁ x^k-1y¹ + ^kC₂ x^k-2 y² + … + ^kC_r x^k-ry^r +….+ ^kC_k x⁰y^k

⇒ (x+y)^k = x^k + ^kC₁ x^k-1y¹ + ^kC₂ x^k-2 y² + … + ^kC_r x^k-ry^r +….+ y^k

Thus the result is true for n = k ≥ 2.

Now consider the expansion for n = k + 1.

(x + y) ^k+1 = (x + y) (x + y)^k

= (x + y) (x^k + ^kC₁ x^k-1y¹ + ^kC₂ x^k-2 y² + … + ^kC_r x^k-ry^r +….+ y^k)

= x^k+1 + (1 + ^kC₁)x^ky + (^kC₁ + ^kC₂) x^k-1y² + … + (^kC_r-1 + ^kC_r) x^k-r+1y^r + … + (^kC_k-1 + 1) xy^k + y^k+1

= x^k+1 + ^k+1C₁x^ky + ^k+1C₂ x^k-1y² + … + ^k+1C_r x^k-r+1y^r + … + ^k+1C_k xy^k + y^k+1 [Because ⁿC_r + ⁿC_r-1 = ⁿ⁺¹C_r]

Thus the result is true for n = k+1. By mathematical induction, this result is true for all positive integers ‘n’. Hence proved.

Properties of Binomial Theorem

• The number of coefficients in the binomial expansion of (x + y)ⁿ is equal to (n + 1).
• There are (n+1) terms in the expansion of (x+y)ⁿ.
• The first and the last terms are xⁿ and yⁿ respectively.
• From the beginning of the expansion of (x + a)ⁿ, the powers of x, decrease from n up to 0, and the powers of a, increase from 0 up to n.
• The general term in the expansion of (x + y) ⁿ is the (r +1)^th term that can be represented as T_r+1, T_r+1 = ⁿC_r x^n-ry^r
• The binomial coefficients in the expansion are arranged in an array, which is called Pascal’s triangle. This pattern developed is summed up by the binomial theorem formula.
• In the binomial expansion of (x + y)ⁿ, the r^th term from the end is (n – r + 2)^th term from the beginning.
• If n is even, then in (x + y)ⁿ the middle term = (n/2)+1 and if n is odd, then in (x + y)ⁿ, the middle terms are (n+1)/2 and (n+3)/2.

Pascal’s Triangle Binomial Expansion

The binomial coefficients are the numbers associated with the variables x, and y in the expansion of (x + y)ⁿ. The binomial coefficients are represented as ⁿC₀, ⁿC₁, ⁿC₂ ….. The binomial coefficients are obtained through the pascal triangle or by using the combinations formula.

Binomial Theorem Coefficients

The values of the binomial coefficients exhibit a specific trend which can be observed in the form of Pascal’s triangle. Pascal’s triangle is an arrangement of binomial coefficients in triangular form. It is named after the French mathematician Blaise Pascal. The numbers in Pascal’s triangle have all the border elements as 1 and the remaining numbers within the triangle are placed in such a way that each number is the sum of two numbers just above the number.

Combinations

The formula for combinations is used to find the value of the binomial coefficients in the expansions using the binomial theorem. The combinations in this case are the different ways of picking r variables from the available n variables. The formula to find the combinations of r objects taken from n different objects is ⁿC_r = n! / [r! (n – r)!]. Here the coefficients have the following properties.

• ⁿC_n = ⁿC₀ = 1
• ⁿC₁ = ⁿC_n-1 = n
• ⁿC_r = ⁿC_r-1

The following properties of binomial expansion can be derived by simply substituting simple numeric values of x = 1 and y = 1 in the binomial expansion of (x + y)ⁿ. The properties of binomial coefficients are as follows.

• C₁ + C₂ + C₃ + C₄ + …….C_n = 2ⁿ
• C₀ + C₂ + C₄ + …. = C₁ + C₃ + C₅ + ……. = 2^n-1
• C₀ – C₁ + C₂ – C₃ + C₄ – C₅ + …. = 0
• C₁ + 2C₂ + 3C₃ + 4C₄ + …….nC_n = n2^n-1
• C₁ – 2C₂ + 3C₃ – 4C₄ + …….(-1)ⁿnC_n = 0
• C₁² + C₂² + C₃² + C₄² + …….C_n² = (2n)! / (n!)²

Important Terms of Binomial Theorem

The following terms related to binomial expansion using the binomial theorem are helpful to find the terms. The details of each of the terms are as follows.

General Term: This term symbolizes all of the terms in the binomial expansion of (x + y)ⁿ. The general term in the binomial expansion of (x + y)ⁿ is T_r+1 = ⁿC_r x^n-ry^r. Here the r-value is one less than the number of the term of the binomial expansion. Also, ⁿC_r is the coefficient, and the sum of the exponents of the variables x and y is equal to n.

Middle Term: The total number of terms in the expansion of (x + y)ⁿ is equal to n + 1. The middle term in the binomial expansion depends on the value of n. The middle term and the number of middle terms depend on the value of n: n is even or odd. For an even value of n there is only one middle term and (n/2 + 1)^th term is the middle term. For an odd value of n, there are two middle terms, and the two middle terms are n/2, and n/2 + 1 terms.

Identifying a Particular Term: There are two simple steps to identify a particular term containing x^p. First, we need to find the general term in the expansion of (x + y)ⁿ. which is is T_r+1 = ⁿC_r x^n-ry^r. Secondly, we need to compare this with x^p to obtain the r-value. Here the r-value is helpful to find the particular term in the binomial expansion. Let us find the fifth term in the expansion of (2x + 3)⁹ using the binomial theorem.

The formula to find the n^th term in the binomial expansion of (x + y)ⁿ is T_r+1 = ⁿC_r x^n-ry^r.

Applying this to (2x + 3)⁹ , T₅ = T₄₊₁ = ⁹C₄ (2x)^9-43⁴. Thus the 5th term is = ⁹C₄ (2x)⁵3⁴

Term Independent of X: The steps to find the term independent of x is similar to finding a particular term in the binomial expansion. First, we need to find the general term in the expansion of (x + y)ⁿ. which is T_r+1 = = ⁿC_r x^n-ry^r. Here to find the term independent of x, we need to find and equalize the exponent of x in the general term to zero. From the obtained value of r, the term independent of x is (r + 1)^th term.

Numerically Greatest Term: The formula to find the numerically greatest term in the expansion of (1 + x)ⁿ is [(n+1) |x|] / (1 + |x|). There are two points to be remembered while using this formula to find the numerically greatest term. First, we need to convert any binomial expansion into the form of (1 + x)ⁿ. We can convert (2x + 3y)⁵ to (1 + 3y/2x)⁵ . Further for this expansion |x| is the numeric value and is equal to 3/2 in this given example. The final answer is rounded to the integral value to obtain the numerically greatest term.

Binomial Expansion for Negative Exponent

The binomial theorem expansion also applies to exponents with negative values. The standard coefficient values of binomial expansion for positive exponents are the same for the expansion with the negative exponents. The terms and the coefficient values remain the same, but the algebraic relationship between the terms varies in the binomial expansion of negative exponents.

• (1 + x)^-1 = 1 – x + x² – x³ + x⁴ – x⁵ + …….
• (1 – x)^-1 = 1 + x + x² + x³ + x⁴ + x⁵ + …….
• (1 + x)^-2 = 1 – 2x + 3x² – 4x³ + ……..
• (1 – x)^-2 = 1 + 2x + 3x² + 4x³ + ……..
• (1 + x)^-3 = 1 – 3x + 6x² – 10x³ + 15x⁴ + ……
• (1 – x)^-3 = 1 + 3x + 6x² + 10x³ + 15x⁴ + ……

Important Notes on Binomial Theorem

The following key points would help in a better understanding of the binomial theorem.

• The number of terms in the binomial expansion of (x + y)ⁿ is equal to n + 1.
• In the expansion of (x + y)ⁿ, the sum of the powers of x and y in each term is equal to n.
• The value of the binomial coefficients from either side of the expansion is equal.
• The number of terms in the binomial expansion of (x + y + z)ⁿ is n(n + 1).

Terms in the Binomial Expansion

In binomial expansion, it is often asked to find the middle term or the general term. The different terms in the binomial expansion that are covered here include

• General Term
• Middle Term
• Independent Term
• Determining a Particular Term
• Numerically Greatest Term
• Ratio of Consecutive Terms/Coefficients

General Term in Binomial Expansion:

We have (x + y)ⁿ = nC₀ xⁿ + nC₁ x^n-1 . y + nC₂ x^n-2 . y² + … + nC_n yⁿ

General Term = T_r+1 = nC_r x^n-r . y^r

• General Term in (1 + x)ⁿ is nC_r x^r
• In the binomial expansion of (x + y)ⁿ, the r^th term from the end is (n – r + 2)^th.

Illustration: Find the number of terms in (1 + 2x +x²)⁵⁰

Sol:

(1 + 2x + x²)⁵⁰ = [(1 + x)²]⁵⁰ = (1 + x)¹⁰⁰

The number of terms = (100 + 1) = 101

Illustration: Find the fourth term from the end in the expansion of (2x – 1/x²)¹⁰

Sol:

Required term =T_{10 – 4 + 2} = T₈ = 10C₇ (2x)³ (−1/x²)⁷ = −960x^-11

Middle Term(s) in the Expansion of (x+y) ^n.n

• If n is even, then (n/2 + 1) Term is the middle term.
• If n is odd then, [(n+1)/2]^th and [(n+3)/2)^th terms are the middle terms.

Illustration: Find the middle term of (1 −3x + 3x² – x³)²ⁿ

Sol:

(1 − 3x + 3x² – x³)²ⁿ = [(1 − x)³]²ⁿ = (1 − x)⁶ⁿ

Middle Term = [(6n/2) + 1] term = 6nC_3n (−x)³ⁿ

Determining a Particular Term:

• In the expansion of (ax^p + b/x^q)ⁿ the coefficient of x^m is the coefficient of T_r+1 where r = [(np−m)/(p+q)]
• In the expansion of (x + a)ⁿ, T_r+1/T_r = (n – r + 1)/r . a/x

Binomial Theorem Examples

Example 1: What is the binomial expansion of (x² + 1)⁵ using the binomial theorem?

Solution:The following formula derived from the Binomial Theorem is helpful to find the expansion.(x + y)ⁿ = (x+y)ⁿ = ⁿC₀ xⁿy⁰ + ⁿC₁ x^n-1y¹ + ⁿC₂ x^n-2 y² + … + ⁿC_k x^n-ky^k +….+ ⁿC_n x⁰yⁿ(x² + 1)⁵ = ⁵C₀ (x²)⁵1⁰ + ⁵C₁ (x²)^5-11¹ + ⁵C₂ (x²)^5-2 1² + ⁵C₃ (x²)^5-3 1³ + ⁵C₄ (x²)^5-4 1⁴ + ⁵C₅ (x²)^5-5 1⁵= x¹⁰ + 5 x⁸ + 10 x⁶ + 10 x⁴ + 5 x² + 1

Answer: (x² + 1)⁵ = x¹⁰ + 5 x⁸ + 10 x⁶ + 10 x⁴ + 5 x² + 1

Example 2: Find the 7^th term in the expansion of (x + 2)¹⁰

Solution:The general term in the expansion of (x+a)ⁿ using the binomial theorem formula isT_r+1 = ⁿC_r x^n-ry^r.Here r = 6, n =10, a = 2Thus by substituting, we getT₇ = T₆₊₁ = ¹⁰C₆ x^10-6 2⁶T₇ = 210 x ⁴ . 64= 13440 x⁴

Answer: 7^th term in (x + 2)¹⁰ is 13440 x⁴

Example 3: Find the coefficient of x² in (x +(1/x))⁸

Solution:Using the binomial theorem formula in the expansion of (x +1/x)⁸, we have x² as the fourth term.⁸C₀ x⁸(1/x)⁰ + ⁸C₁ x⁷(1/x)¹ + ⁸C₂ x⁶(1/x)² + ⁸C₃ x⁵(1/x)³ + ⁸C₄ x⁴(1/x)⁴ + ⁸C₅ x³(1/x)⁵ + ⁸C₆ x²(1/x)⁶ + ⁸C₇ x¹(1/x)⁷ + ⁸C₈ x⁰(1/x)⁸ +The coefficient of the fourth term is ⁸C₃= 56

Answer: The coefficient of x² in the expansion of (x + (1/x))⁸ is 56

Binomial Theorem Statement

The binomial theorem is the method of expanding an expression that has been raised to any finite power. A binomial theorem is a powerful tool of expansion which has applications in Algebra, probability, etc.

Binomial Expression: A binomial expression is an algebraic expression that contains two dissimilar terms. Eg.., a + b, a³ + b³, etc.

Binomial Expansion Formula: Let n ∈ N,x,y,∈ R then

(x + y)ⁿ = ⁿΣ_r=0 nC_r x^{n – r} · y^r where,

Illustration 1: Expand (x/3 + 2/y)⁴

Sol:

Illustration 2: (√2 + 1)⁵ + (√2 − 1)⁵

Sol:

We have

(x + y)⁵ + (x – y)⁵ = 2[5C₀  x⁵ + 5C₂  x³ y²  +  5C₄ xy⁴]

= 2(x⁵ + 10 x³ y² + 5xy⁴)

Now (√2 + 1)⁵ + (√2 − 1)⁵ = 2[(√2)⁵ + 10(√2)³(1)² + 5(√2)(1)⁴]

=58√2

Binomial Expansion Formulas

To find binomial coefficients, we can also use Pascal’s Triangle.

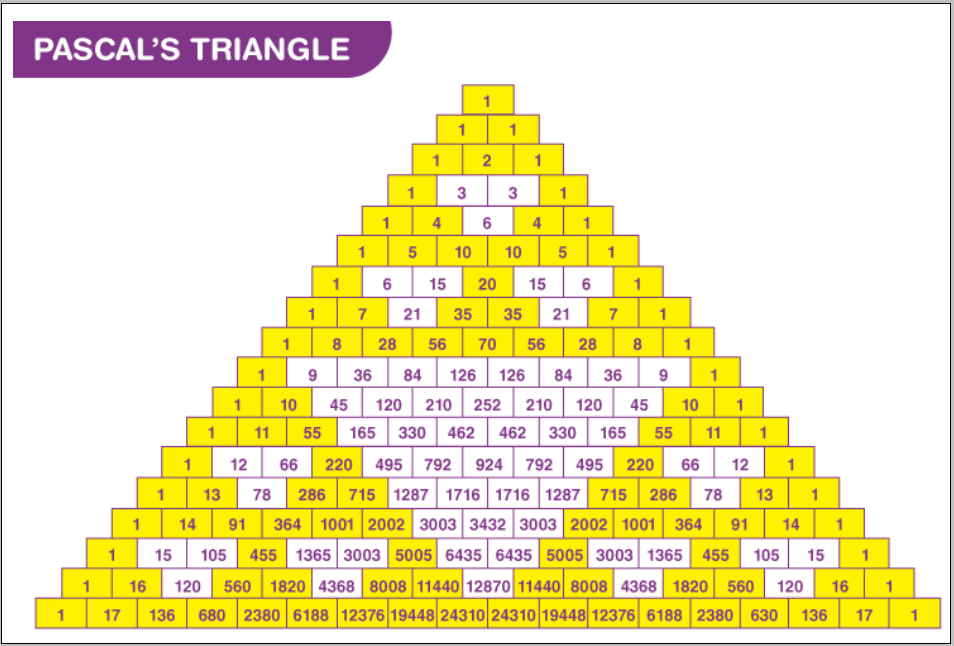
Some other useful expansions:

• (x + y)ⁿ + (x−y)ⁿ = 2[C₀ xⁿ + C₂ x^n-1 y² + C₄ x^n-4 y⁴ + …]
• (x + y)ⁿ – (x−y)ⁿ = 2[C₁ x^n-1 y + C₃ x^n-3 y³ + C₅ x^n-5 y⁵ + …]
• (1 + x)ⁿ  = ⁿΣ_r-0 nC_r . x^r = [C₀ + C₁ x + C₂ x² + … C_n x_n]
• (1+x)ⁿ + (1 − x)ⁿ = 2[C₀ + C₂ x²+C₄ x⁴ + …]
• (1+x)ⁿ − (1−x)ⁿ = 2[C₁ x + C₃ x³ + C₅ x⁵ + …]
• The number of terms in the expansion of (x + a)ⁿ + (x−a)ⁿ is (n+2)/2 if “n” is even or (n+1)/2 if “n” is odd.
• The number of terms in the expansion of (x + a)ⁿ − (x−a)ⁿ  is (n/2) if “n” is even or (n+1)/2 if “n” is odd.

Properties of Binomial Coefficients

Binomial coefficients refer to the integers, which are coefficients in the binomial theorem. Some of the most important properties of binomial coefficients are:

• C₀ + C₁ + C₂ + … + C_n = 2ⁿ
• C₀ + C₂ + C₄ + … = C₁ + C₃ + C₅ + … = 2^n-1
• C₀ – C₁ + C₂ – C₃ + … +(−1)ⁿ . nC_n = 0
• nC₁ + 2.nC₂ + 3.nC₃ + … + n.nC_n = n.2^n-1
• C₁ − 2C₂ + 3C₃ − 4C₄ + … +(−1)^n-1 C_n = 0 for n > 1
• C₀² + C₁² + C₂² + …C_n² = [(2n)!/ (n!)²]

Illustration: If (1 + x)¹⁵ = a₀ + a₁x + . . . . .  + a₁₅ x¹⁵ then, find the value of 

Sol:

= C₁/C₀ + 2 C₂/C₁+ 3C₃/C₂ + . . . . + 15 C₁₅/C₁₄

= 15 + 14 + 13 + . . . . . + 1 = [15(15+1)]/2 = 120

Independent Term

The term Independent of in the expansion of [ax^p + (b/x^q)]ⁿ is

T_r+1 = ⁿC_r a^n-r b^r, where r = (np/p+q) (integer)

Illustration: Find the independent term of x in (x+1/x)⁶

Sol:

r = [6(1)/1+1] = 3

The independent term is 6C₃ = 20

Illustration: Find the independent term in the expansion of:

Sol:

(x^1/3 + 1 – 1 – 1/√x)¹⁰ = (x^1/3 – 1/√x)¹⁰

r = [10(1/3)]/[1/3+1/2] = 4

∴ T₅ = ¹⁰C₄ = 210

Numerically Greatest Term in the Expansion of (1+x)ⁿ:

• If [(n+1)|x|]/[|x|+1] = P, is a positive integer, then the P^th term and (P+1)^th terms are numerically the greatest terms in the expansion of (1+x)ⁿ
• If[(n+1)|x|]/[|x|+1] = P + F, where P is a positive integer, and 0 < F < 1, then (P+1)^th term is numerically the greatest term in the expansion of (1+x)ⁿ.

Illustration: Find the numerically greatest term in (1-3x)¹⁰ when x = (1/2)

Sol:

[(n + 1)|α|] / [|α| + 1] = (11 × 3/2)/(3/2+1) = 33/5 = 6.6

Therefore, T₇ is the numerically greatest term.

T_{6 + 1} = 10C₆ . (−3x)⁶ = 10C₆ . (3/2)⁶

Ratio of Consecutive Terms/Coefficients:

The coefficients of x^r and x^{r + 1} are nC_{r – 1} and nC_r, respectively.

(nC_r / nC_{r – 1}) = (n – r + 1) / r

Illustration: If the coefficients of three consecutive terms in the expansion of (1+x)ⁿ are in the ratio 1:7:42, then find the value of n.

Sol:

Let (r – 1)^th, (r)^th and (r + 1)^th be the three consecutive terms.

Then, the given ratio is 1:7:42

Now (nC_r-2 / nC_{r – 1}) = (1/7)

(nC_r-2 / nC_{r – 1}) = (1/7) ⇒ [(r – 1)/(n − r+2)] = (1/7) ⇒ n−8r+9=0 → (1)

And,

(nC_r-1 / nC_r) = (7/42) ⇒ [(r)/(n – r +1)] =(1/6) ⇒ n−7r +1=0 → (2)

From (1) & (2), n = 55

Applications of Binomial Theorem

The binomial theorem has a wide range of applications in Mathematics, like finding the remainder, finding the digits of a number, etc. The most common binomial theorem applications are as follows:

Finding Remainder Using Binomial Theorem

Illustration: Find the remainder when 7¹⁰³ is divided by 25.

Sol:

(7¹⁰³ / 25) = [7(49)⁵¹ / 25)] = [7(50 − 1)⁵¹ / 25]

= [7(25K − 1) / 25] = [(175K – 25 + 25−7) / 25]

= [(25(7K − 1) + 18) / 25]

∴ The remainder = 18

Illustration: If the fractional part of the number (2⁴⁰³ / 15) is (K/15), then find K.

Sol:

(2⁴⁰³ / 15) = [2³ (2⁴)¹⁰⁰ / 15]

= 8/15 (15 + 1)¹⁰⁰ = 8/ 15 (15λ + 1) = 8λ + 8/15

∵ 8λ is an integer, fractional part = 8/15

So, K = 8.

Finding Digits of a Number

Illustration: Find the last two digits of the number (13)¹⁰

Sol:

(13)¹⁰ = (169)⁵ = (170 − 1)⁵

= 5C₀ (170)⁵ − 5C₁ (170)⁴ + 5C₂ (170)³ − 5C₃ (170)² + 5C₄ (170) − 5C₅

= 5C₀ (170)⁵ − 5C₁ (170)⁴ + 5C₂ (170)³ − 5C₃ (170)² + 5(170) − 1

A multiple of 100 + 5(170) – 1 = 100K + 849

∴ The last two digits are 49.

Relation between Two Numbers

Illustration: Find the larger of 99⁵⁰ + 100⁵⁰ and 101⁵⁰

Sol:

101⁵⁰ = (100 + 1)⁵⁰ = 100⁵⁰ + 50 . 100⁴⁹ + 25 . 49 . 100⁴⁸ + …

⇒ 99⁵⁰ = (100 − 1)⁵⁰ = 100⁵⁰ – 50 . 100⁴⁹ + 25 . 49 . 100⁴⁸ − ….

⇒ 101⁵⁰ – 99⁵⁰ = 2[50 . 100⁴⁹ + 25(49) (16) 100⁴⁷ + …]

= 100⁵⁰ + 50 . 49 . 16 . 100⁴⁷ + … >100⁵⁰

∴ 101⁵⁰ – 99⁵⁰ > 100⁵⁰

⇒ 101⁵⁰ > 100⁵⁰ + 99⁵⁰

Divisibility Test

Illustration: Show that 11⁹ + 9¹¹ is divisible by 10.

Sol:

11⁹ + 9¹¹ = (10 + 1)⁹ + (10 − 1)¹¹

= (9C₀ . 10⁹ + 9C₁ . 10⁸ + … 9C₉) + (11C₀ . 10¹¹ − 11C₁ . 10¹⁰ + … −11C₁₁)

= 9C₀ . 10⁹ + 9C₁ . 10⁸ + … + 9C₈ . 10 + 1 + 10¹¹ − 11C₁ . 10¹⁰ + … + 11C₁₀ . 10−1

= 10[9C₀ . 10⁸ + 9C₁ . 10⁷ + … + 9C₈ + 11C₀ . 10¹⁰ − 11C₁ . 10⁹ + … + 11C₁₀]

= 10K, which is divisible by 10.

Formulae:

• The number of terms in the expansion of (x₁ + x₂ + … x_r)ⁿ is (n + r − 1)C_{r – 1}
• The sum of the coefficients of (ax + by)ⁿ is (a + b)ⁿ

If f(x) = (a₀ + a₁x + a₂x² + …. + a_mx^m)ⁿ then

• (a) Sum of coefficients = f(1)
• (b) Sum of coefficients of even powers of x is: [f(1) + f(−1)] / 2
• (c) Sum of coefficients of odd powers of x is [f(1) − f(−1)] / 2

Binomial Theorem for Any Index

Let n be a rational number and x be a real number, such that | x | < 1. Then,

Proof:

Let f(x) = (1 + x)ⁿ = a₀ + a₁ x + a₂ x² + … +a_r x^r + … (1)

f(0) = (1 + 0)ⁿ = 1

Differentiating (1) w.r.t. x on both sides, we get

n(1 + x)^{n – 1}

= a₁ + 2a₂ x + 3a₃ x³ + 4a₄ x³ + … + ra_r x^{r – 1} + … (2)

Put x = 0, we get n = a₁

Differentiating (2) w.r.t. x on both sides, we get

n(n − 1)(1 + x)^{n – 2}

= 2a₂ + 6a₃ x + 12a₄ x² + … + r(r−1) a_r x^{r – 2} + … (3)

Put x = 0, we get a₂ = [n(n−1)] / 2!

Differentiating (3), w.r.t. x on both sides, we get

n(n − 1)(n − 2)(1 + x)^{n – 3} = 6a₃ + 24a₄ x + … + r(r − 1)(r − 2) a_r x_{r – 3} + …

Put x = 0, we get a₃ = [n(n−1)(n−2)] / 3!

Similarly, we get a₄ = [n(n−1)(n−2)(n−3)] / r! and so on

∴ a_r = [n(n−1)(n−2)…(n−r+1)] / r!

Putting the values of a₀, a₁, a₂, a₃, …, a_r obtained in (1), we get

(1 + x)ⁿ = 1 + nx + [{n(n−1)} / 2!] x² + [{n(n − 1)(n − 2)} / 2!] x³ + … + [{n(n − 1)(n − 2) … (n – r + 1)}/ r!] x^r + …

Binomial Theorem for Rational Index

The number of rational terms in the expression of (a^1/l + b^1/k )ⁿ is [n / LCM of {l,k}] when none of and is a factor of and when at least one of and is a factor of is [n / LCM of {l,k}] + 1 where [.] is the greatest integer function.

Illustration: Find the number of irrational terms in (⁸√5 + ⁶√2)¹⁰⁰.

Sol:

T_{r + 1} = 100C_r (⁸√5)^{100 – r} . (⁶√2)^r = 100C_r . 5[(100 – r)/8] .2^r/6.

∴ r = 12,36,60,84

The number of rational terms = 4

The number of irrational terms = 101 – 4 = 97

Binomial Theorem for Negative Index

1. If the rational number and -1 < x <1, then,

• (1 − x)^-1 = 1 + x + x² + x³ + … + x^r + … ∞
• (1 + x)^-1 = 1 – x + x² – x³ + … (−1)^r x^r+ … ∞
• (1 − x)^-2 = 1 + 2x + 3x² − 4x³ + … + (r + 1)x^r + … ∞
•  (1 + x)^-2 = 1 − 2x + 3x² − 4x³ + … + (−1)^r (r + 1)x^r + … ∞

2. Number of terms in (1 + x)ⁿ is

• ‘n+1 when positive integer.
• Infinite when is not a positive integer & | x | < 1

3. First negative term in (1 + x)^p/q when 0 < x < 1, p, q are positive integers & ‘p’ is not a multiple of ‘q’ is T_[p/q] + 3

Multinomial Theorem

Using the binomial theorem, we have

(x + a)ⁿ

=ⁿ∑_{r = 0}nC_r x^{n – r} a^r, n∈N

= ⁿ∑_{r = 0} [n! / (n − r)!r!] x^{n – r}a^r

= ⁿ∑_{r + s =n} [n! / r!s!] x^s a^r, where s = n – r.

This result can be generalised in the following form:

(x₁ + x₂ + … +x_k)ⁿ

= ∑_{r1 + r2 + …. + rk = n} [n! / r1!r2!…rk!] x₁^r1 x₂^r2 …x_k^rk

The general term in the above expansion is

[(n!) / (r₁! r₂! r₃! … r_k!)] x₁^r1 x₂^r2 x₃^r3… x_k^rk

The number of terms in the above expansion is equal to the number of non-negative integral solutions of the equation.

r₁+r₂ + … + r_k = n, because each solution of this equation gives a term in the above expansion. The number of such solutions is ^{n + k – 1}C_k −1.

PARTICULAR CASES

Case-1:

The above expansion has ^n+3-1C_3-1 = ^{n + 2}C₂ terms.

Case-2: 

There are ^{n + 4 – 1}C_{4 – 1} = ^{n + 3}C₃ terms in the above expansion.

REMARK: The greatest coefficient in the expansion of (x₁ + x₂ + … + x_m)ⁿ is [(n!) / (q!)^{m – r}{(q+1)!}^r], where q and r are the quotient and remainder, respectively, when n is divided by m.

Multinomial Expansions

Consider the expansion of (x + y + z)¹⁰. In the expansion, each term has different powers of x, y, and z, and the sum of these powers is always 10.

One of the terms is λx²y³z⁵. Now, the coefficient of this term is equal to the number of ways 2x′s, 3y′s, and 5z′s are arranged, i.e., 10! (2! 3! 5!). Thus,

(x+y+z)¹⁰ = ∑(10!) /  (P1! P2! P3!) x^P1 y^P2 z^P3

Where P1 + P2 + P3 = 10 and 0 ≤ P1, P2, P3 ≥ 10

In general,

(x₁ + x₂ + … x_r)ⁿ = ∑ (n!) / (P1! P2! … Pr!) x^P1 x^P2 … x^Pr

Where P1 + P2 + P3 + … + Pr = n and 0 ≤ P1, P2, … Pr ≥ n

Number of Terms in the Expansion of (x₁ + x₂ + … + x_r)ⁿ

From the general term of the above expansion, we can conclude that the number of terms is equal to the number of ways different powers can be distributed to x₁, x₂, x₃ …., x_n, such that the sum of powers is always “n”.

The number of non-negative integral solutions of x₁ + x₂ + … + x_r = n is ^{n +r – 1}C_{r – 1}.

For example, the number of terms in the expansion of (x + y + z)³ is ^{3 + 3 -1}C_{3 – 1} =  ⁵C₂ = 10

As in the expansion, we have terms such as

As x⁰ y⁰ z⁰, x⁰ y¹ z², x⁰ y² z¹, x⁰ y³ z⁰, x¹ y⁰ z², x¹ y¹ z¹, x¹ y² z⁰, x² y⁰ z¹, x² y¹ z⁰, x³ y⁰ z⁰.

The number of terms in (x + y + z)ⁿ is ^{n + 3 – 1}C_{3 – 1} = ^{n + 2}C₂.

The number of terms in (x + y + z + w)ⁿ is ^{n + 4 – 1}C_{4 – 1} = ^{n + 3}C₃ and so on.

Problems on Binomial Theorem

Question 1: If the third term in the binomial expansion of

equals 2560, find x.

Solution:

⇒ (log₂^x)² = 4

⇒ log₂^x = 2 or -2

⇒ x = 4 or 1/4.

Question 2: Find the positive value of λ for which the coefficient of x² in the expression x²[√x + (λ/x²)]¹⁰ is 720.

Solution:

⇒ x² [¹⁰C_r . (√x)^10-r . (λ/x²)^r] = x² [¹⁰C_r . λ^r . x^(10-r)/2 . x^-2r]

= x² [¹⁰C_r . λ^r . x^(10-5r)/2]

Therefore, r = 2

Hence, ¹⁰C₂ . λ² = 720

⇒ λ² = 16

⇒ λ = ±4.

Question 3: The sum of the real values of x for which the middle term in the binomial expansion of (x³/3  + 3/x)⁸ equals 5670 is?

Solution:

T₅ = ⁸C₄ × (x¹²/81) × (81/x⁴) = 5670

⇒ 70 x⁸ = 5670

⇒ x = ± √3.

Question 4: Let (x + 10)⁵⁰ + (x – 10)⁵⁰ = a₀ +a₁x + a₂ x₂ + . . . . . + a₅₀ x⁵⁰ for all x ∈R, then a₂/a₀ is equal to?

Solution:

⇒ (x + 10)⁵⁰ + (x – 10)⁵⁰:

a₂ = 2 × ⁵⁰C₂ × 10⁴⁸

a₀ = 2 × 10⁵⁰

⇒ a₂/a₀ = ⁵⁰C₂/10² = 12.25.

Question 5: Find the coefficient of x⁹ in the expansion of (1 + x) (1 + x² ) (1 + x³) . . . . . . (1 + x¹⁰⁰).

Solution:

x⁹ can be formed in 8 ways.

i.e., x⁹ x¹⁺⁸ x²⁺⁷ x³⁺⁶ x⁴⁺⁵, x¹⁺³⁺⁵, x²⁺³⁺⁴

∴ The coefficient of x⁹ = 1 + 1 + 1 + . . . . + 8 times = 8.

Question 6: The coefficients of three consecutive terms of (1 + x)ⁿ⁺⁵ are in the ratio 5:10:14. Find n.

Solution:

Let T_r-1, T_r, T_r+1 are three consecutive terms of (1 + x)ⁿ⁺⁵

⇒  T_r-1 = (n+5) C_r-2 . x^r-2

⇒  T_r = (n+5) C_r-1 . x^r-1

⇒  T_r+1 = (n+5) C_r . x^r

Given

(n+5) C_r-2 : (n+5) C_r-1 : (n+5) C_r = 5 : 10 : 14

Therefore, [(n+5) C_r-2]/5= [(n+5) C_r-1]/10 = (n+5) C_r/14

Comparing first two results we have n – 3r = -9 . . . . . . (1)

Comparing last two results we have 5n – 12r = -30 . . . . . .  (2)

From equations (1) and (2), n = 6

Question 7: The digit in the units place of the number 183! + 3¹⁸³.

Solution:

⇒ 3¹⁸³ = (3⁴)⁴⁵.3³

⇒ unit digit = 7 and 183! ends with 0

∴ The units digit of  183! + 3¹⁸³ is 7.

Question 8: Find the total number of terms in the expansion of (x + a)¹⁰⁰ + (x – a)¹⁰⁰.

Solution:

⇒ (x + a)¹⁰⁰ + (x – a)¹⁰⁰ = 2[¹⁰⁰C₀ x¹⁰⁰. ¹⁰⁰C₂  x⁹⁸ . a² + . . . . . . +  ¹⁰⁰C₁₀₀ a¹⁰⁰]

∴ Total Terms = 51

Question 9: Find the coefficient of t⁴ in the expansion of [(1-t⁶)/(1 – t)].

Solution:

⇒ [(1-t⁶)/(1 – t)] = (1 – t¹⁸ – 3t⁶ + 3t¹²) (1 – t)^-3

Coefficient of t in (1 – t)^-3 = 3 + 4 – 1

C₄ = ⁶C₂ =15

The coefficient of x^r in (1 – x)^-n = (r + n – 1) C_r

Question 10: Find the ratio of the 5^th term from the beginning to the 5^th term from the end in the binomial expansion of  [2^1/3 + 1/{2.(3)^1/3}]¹⁰.

Solution:

Question 11: Find the coefficient of a³b²c⁴d in the expansion of (a-b-c+d)¹⁰.

Solution:

Expand (a – b – c + d)¹⁰ using the multinomial theorem, and by using the coefficient property, we can obtain the required result.

Using the multinomial theorem, we have

We want to get coefficient of a³b²c⁴d this implies that r₁ = 3, r₂ = 2, r₃ = 4, r₄ = 1,

∴ The coefficient of a³b²c⁴d is [(10)!/(3!.2!.4)] (-1)² (-1)^-4 = 12600

Question 12: Find the coefficient of in the expansion of (1 + x + x² +x³)¹¹.

Solution:

By expanding the given equation using the expansion formula, we can get the coefficient x⁴

i.e. 1 + x + x² + x³ = (1 + x) + x² (1 + x) = (1 + x) (1 + x²)

⇒ (1 + x + x² + x³) x¹¹ = (1+x)¹¹ (1+x²)¹¹

= 1+ ¹¹C₁ x² + ¹¹C₂ x² + ¹¹C₃ x³ + ¹¹C₄ x⁴ . . . . . . .

= 1 + ¹¹C₁ x² + ¹¹C₂ x⁴ + . . . . . .

To find the term in from the product of two brackets on the right-hand-side, consider the following products terms as

= 1 × ¹¹C₂ x⁴ + ¹¹C₂ x² × ¹¹C₁ x² + ¹¹C₄ x⁴

= ¹¹C₂ + ¹¹C₂ × ¹¹C₁ + ¹¹C₄ ] x⁴

⇒ [55 + 605 + 330] x⁴ = 990x⁴

∴ The coefficient of x⁴ is 990.

Question 13: Find the number of terms free from the radical sign in the expansion of (√5 + ⁴√n)¹⁰⁰.

Solution:

T_r+1 = ¹⁰⁰C_r . 5^{(100 – r)/2} n^r/4

Where r = 0, 1, 2, . . . . . . , 100

r must be 0, 4, 8, … 100

The number of rational terms = 26

Question 14: Find the degree of the polynomial [x + {√(3^(3-1))}^1/2]⁵ + [x + {√(3^(3-1))}^1/2]⁵.

Solution:

[x + { √(3^(3-1)) }^1/2 ]⁵:

= 2 [⁵C₀ x⁵ + ⁵C₂ x⁵ (x³ – 1) + ⁵C₄ . x . (x³ – 1)²]

Therefore, the highest power = 7.

Question 15: Find the last three digits of 27²⁶.

Solution:

By reducing 27²⁶ into the form (730 – 1)ⁿ and using simple binomial expansion, we will get the required digits.

We have 27² = 729

Now 27²⁶ = (729)¹³ = (730 – 1)¹³

= ¹³C₀ (730)¹³ – ¹³C₁ (730)¹² + ¹³C₂ (730)¹¹ – . . . . . – ¹³C₁₀ (730)³ + ¹³C₁₁(730)² – ¹³C₁₂ (730) + 1

= 1000m + [(13 × 12)]/2] × (14)² – (13) × (730) + 1

Where ‘m’ is a positive integer

= 1000m + 15288 – 9490 = 1000m + 5799

Thus, the last three digits of 17²⁵⁶ are 799.

FAQs on Binomial Theorem

What Is the Binomial Theorem?

The binomial theorem is used for the expansion of the algebraic terms of the form(x + y)ⁿ . (x+y)ⁿ = ⁿC₀ xⁿy⁰ + ⁿC₁ x^n-1y¹ + ⁿC₂ x^n-2 y² + … + ⁿC_n-1 x¹y^n-1 + ⁿC_n x⁰yⁿ. Here the number of terms in the binomial expansion having an exponent of n is n + 1. The exponent of the first term in the expansion is decreasing and the exponent of the second term in the expansion is increasing in a progressive manner. The coefficients of the binomial expansion can be found from the pascals triangle or using the combinations formula of ⁿC_r = n! / [r! (n – r)!].

What Is the Constant Term in the Binomial Theorem?

The constant term in the binomial expansion is a numeric value and is independent of the variables. For a binomial expansion of (x + y)ⁿ the term independent of x can be calculated by finding the term independent of x.

What Is the Coefficient in the Binomial Theorem?

The coefficients in the binomial expansion are ⁿC₀, ⁿC₁, ⁿC₂, ….ⁿC_r ……ⁿC_n. The coefficient value for n = 4 is equal to 1, 4, 6, 4,1, and the coefficient value for n = 5 is 1, 5, 10, 20, 10, 5, 1. The coefficient values can be found either from the pascals triangle or by using the combinations formula of ⁿC_r = n! / [r! (n – r)!].

Where Is Binomial Theorem Used?

The binomial theorem is useful to do the binomial expansion and find the expansions for the algebraic identities. Further, the binomial theorem is also used in probability for binomial expansion. A few of the algebraic identities derived using the binomial theorem are as follows.

• (a + b)² = a² + 2ab + b²
• (a – b)² = a² – 2ab + b²
• (a + b)(a – b) = a² – b²
• (a + b)³ = a³ +3a²b + 3ab² + b³
• (a – b)³ = a³ – 3a²b + 3ab² – b³
• (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ac

What Is the General Term in Binomial Theorem?

The general term of the binomial expansion of (x + y)ⁿ is T_r+1 = ⁿC_r x^n-ry^r.. The r-value for the term is one less than the number of the term. In the general term, the sum of the exponents of both the terms is equal to n. Further, the general term is helpful to derive the independent term, the numerically greatest term, and the term with particular power.

How to Find Terms in Binomial Theorem?

The number of terms in a binomial expansion with an exponent of n is equal to n + 1. Further to find a particular term in the expansion of (x + y)ⁿ we make use of the general term formula. The general term of the binomial expansion is T_r+1 = ⁿC_r x^n-ry^r. . Here the coefficient values are found from the pascals triangle or using the combinations formula, and the sum of the exponents of both the terms in the general term is equal to n.

How Do You Find the Number of Terms in the Expansion using the Binomial Theorem Formula?

The number of terms in the binomial expansion of (x+a)ⁿ is n+1 terms. i.e. add 1 to the power, the binomial coefficient is raised to. If we expand (2x+5)¹⁰, we will have 10 +1 = 11 terms on expansion.

How to Find Number of Terms in Binomial Theorem?

The number of terms in the binomial expansion is one more than the exponent value. The number of terms in the expansion of (x + y)ⁿ is equal to (n + 1).

What Is the Middle Term in Binomial Theorem?

The middle term in the binomial expansion depends on the value of n. The middle term and the number of middle terms depend on the value of n: n is even or odd. For an even value of n there is only one middle term and (n/2 + 1) term is the middle term. For an odd value of n, there are two middle terms, and the two middle terms are n/2, and n/2 + 1 terms.

What Is the General Form of Binomial Theorem Formula?

The general formula of binomial theorem formula is used in the expansion of binomial expression of the form:

(x+y)ⁿ = ⁿC₀ xⁿy⁰ + ⁿC₁ x^n-1y¹ + ⁿC₂ x^n-2 y² + … + ⁿC_k x^n-ky^k +….+ ⁿC_n x⁰yⁿ,
where,

• x, y, n are natural numbers, and,
• 0 < k ≤ n

Where Is Binomial Theorem Formula Used?

The binomial theorem formula is used to expand the binomial expressions. We apply the formula in finding probability, combinatorics, calculus, and in other important areas of math. For example, (101)⁵ =(100+1)⁵ = 100⁵+ 5 × 100⁴ + 10 × 100³+ 10 × 100²+ 5 × 100 + 1 = 10,000,000,000+ 500,000,000 + 10,000,000 + 100,000 + 500 +1 = 10,510,100,501

What Is n and r in The Binomial Theorem Formula?

In the binomial theorem formula of expansion (x+a)ⁿ, we use the combinatorics formula that is denoted as ⁿC_r, where n is the exponent in the expansion and r is the term number that ranges from 0 to n.

Give the binomial theorem formula.

We use the binomial theorem to find the expansion of the algebraic terms of the form(x + y)ⁿ. The formula is (x + y)ⁿ = Σ_r=0^n  nC_r x^{n – r} · y^r.

What is the general term in a binomial expansion?

The general term of a binomial expansion is T_r+1 = ⁿC_r x^n-r y^r.

What is the number of terms in the expansion of (x + a)ⁿ + (x-a)ⁿ ?

The number of terms in the expansion of (x + a)ⁿ + (x-a)ⁿ is (n+2)/2 if n is even or (n+1)/2 if n is odd.

List two applications of the binomial theorem.

In Mathematics, the binomial theorem is used to find the remainder and also find the digits of a number.

FORMULAS Related Links

Binomial Expansion Formula

✅ Binomial Distribution Formula ⭐️⭐️⭐️⭐️⭐

✅ Binomial Probability Formula ⭐️⭐️⭐️⭐️⭐

Binomial Theorem Formula